How Does Music Theory Help With Math

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for AudioLover.com, at no extra cost. Learn more)

Introduction

Music theory is a fascinating and complex field of study that explores the principles and techniques behind the structure, notation, and performance of music. It delves into the intricate relationship between notes, chords, scales, rhythm, and harmony, allowing musicians to create captivating melodies and harmonies.

But did you know that music theory also has a profound impact on other areas of knowledge? One such area is mathematics. The relationship between music theory and math is a symbiotic one, with each discipline enhancing the other. In fact, several studies have shown that studying music theory can significantly improve mathematical skills and problem-solving abilities.

While it may seem surprising at first, the overlap between music theory and math is not as arbitrary as it seems. Both disciplines share fundamental principles such as structure, patterns, and logic. By delving into the world of music theory, musicians and math enthusiasts alike can unlock new pathways for understanding and enhancing their mathematical abilities.

In this article, we will explore the ways in which music theory helps with math. We will examine how the study of music theory enhances cognitive skills, develops problem-solving abilities, improves spatial reasoning skills, enhances pattern recognition, and improves numerical reasoning skills. Additionally, we will explore how music theory principles can be applied to mathematical problem-solving to make complex concepts more accessible.

Whether you are a musician looking to strengthen your understanding of math or a math enthusiast curious about the benefits of music theory, this article will provide valuable insights into the fascinating connection between these two disciplines.

The Relationship Between Music Theory and Math

Music theory and math have a deep-rooted relationship that goes beyond mere coincidence. Both disciplines rely on similar principles and concepts, making them interconnected in several ways.

One of the key connections between music theory and math is in their shared foundation of structure and patterns. In music, composers and performers rely on understanding the underlying structure of a piece, including the arrangement of notes, chords, and rhythms. Similarly, in math, patterns and structures are the building blocks for solving problems and identifying relationships between numbers or variables.

Furthermore, both music theory and math require logical thinking and reasoning. In music theory, musicians use logical reasoning to analyze a composition and make decisions about its performance. In math, logical thinking is essential for solving complex equations or proofs.

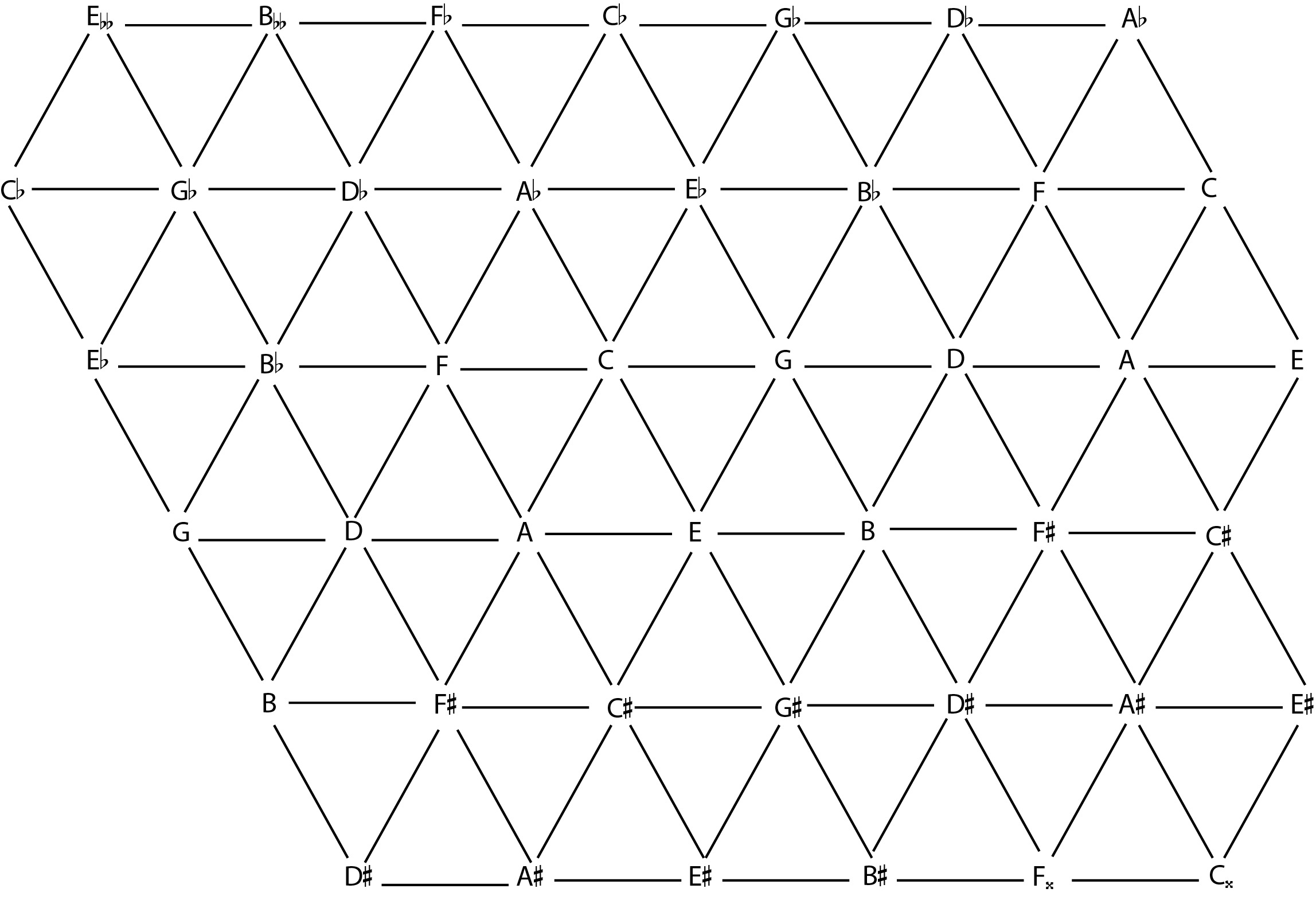
Another pivotal link between music theory and math is found in the concept of ratios and proportions. In music theory, intervals such as octaves, fifths, and thirds are based on specific ratios between frequencies. Similarly, math involves the use of ratios and proportions to compare quantities and solve problems. This shared use of ratios and proportions underscores the inherent mathematical nature of music theory.

Additionally, both disciplines emphasize precision and accuracy. In music theory, a slight change in a note or rhythm can drastically alter the meaning and impact of a musical phrase. Similarly, in math, precision is crucial for obtaining accurate results. The attention to detail required in both music theory and math fosters a disciplined and meticulous mindset.

The relationship between music theory and math extends beyond theoretical connections. Several studies have demonstrated a positive correlation between the study of music theory and mathematical ability. Engaging with music theory exercises the brain in ways that promote mathematical thinking and problem-solving skills. The analytical thinking, pattern recognition, and abstract reasoning developed through music theory can be directly applied to mathematical concepts and calculations.

Overall, the relationship between music theory and math is a dynamic and mutually beneficial one. By bridging these disciplines and exploring their shared principles and concepts, individuals can enhance their understanding and proficiency in both areas.

Enhancing Cognitive Skills with Music Theory

Studying music theory not only enhances musical abilities but also provides a range of cognitive benefits. The intricate nature of music theory exercises the brain, leading to improved cognitive skills that extend beyond the realm of music.

One cognitive skill that music theory enhances is memory. Musicians must memorize musical notation, scales, chords, and patterns to perform pieces accurately. This constant engagement with memorization exercises strengthens memory capacity and recall abilities, leading to improved memory performance in other areas as well.

Music theory also enhances auditory processing skills. Musicians learn to discern different sounds, tones, and nuances in music, allowing them to develop a finely tuned ear. This heightened auditory perception translates to improved language processing skills, as musicians are more adept at differentiating and understanding speech sounds.

Furthermore, music theory promotes analytical thinking and problem-solving skills. As musicians analyze musical compositions, they must identify patterns, structures, and relationships between notes and chords. This analytical approach trains the brain to think critically, identify underlying patterns, and solve complex problems in a logical and systematic way.

Music theory also nurtures creativity. When musicians compose or improvise, they engage in a creative process that involves exploring different melodies, harmonies, and rhythms. This constant exercise of imagination and creativity stimulates the brain, leading to enhanced creative thinking skills that can be applied to various aspects of life, including problem-solving and innovative thinking.

Lastly, music theory promotes multitasking skills. Musicians must simultaneously read musical notation, interpret rhythm, listen to others in an ensemble, and produce their own sound. This multitasking ability translates to improved multitasking in daily life, allowing individuals to juggle multiple tasks and responsibilities effectively.

The cognitive benefits of music theory extend beyond the realm of musicianship. Studies have shown a positive correlation between music education and academic achievement, particularly in areas such as math, science, and language arts. The cognitive skills developed through music theory provide a solid foundation for learning and contribute to overall academic success.

By engaging with music theory, individuals can enhance their memory, auditory processing, analytical thinking, creativity, and multitasking skills. These cognitive benefits not only enhance musical abilities but also have a positive impact on various areas of life, unlocking new pathways for learning and personal growth.

Developing Problem-Solving Abilities through Music Theory

Music theory is not just about understanding the technical aspects of music; it is also a powerful tool for developing problem-solving abilities. The analytical nature of music theory fosters a mindset that is conducive to tackling complex problems in a logical and systematic way.

One way in which music theory develops problem-solving abilities is through the analysis of musical compositions. Musicians engage in critical analysis, dissecting the structure, harmony, and form of a piece to gain insights into the composer’s intentions. This analytical approach trains the brain to break down complex problems into smaller, more manageable components, allowing for a more systematic problem-solving process.

Moreover, music theory requires musicians to think creatively and find innovative solutions. When faced with a musical challenge, such as improvising or composing, musicians must think outside the box to create something unique and compelling. This creative problem-solving fosters a mindset that is open to exploring different perspectives and generating novel ideas, skills that are valuable in solving problems across various domains.

Music theory also develops problem-solving abilities through the application of theory to performance. Musicians must navigate through musical scores, interpreting notation, dynamics, and expressions to bring a piece to life. This process involves making musical decisions, such as phrasing, articulation, and interpretation, which require problem-solving skills to create a compelling and expressive performance.

Furthermore, music theory cultivates problem-solving abilities through the study of harmony and chord progressions. Musicians learn to analyze and understand the relationships between chords, and how different chord progressions create tension and resolve. This understanding of musical tension and resolution translates to problem-solving in other domains, as musicians are adept at identifying patterns, recognizing relationships, and finding solutions that bring balance and coherence.

Studies have shown that individuals who engage with music theory and actively participate in music-making activities demonstrate improved problem-solving skills in non-musical tasks. The skills developed through music theory, such as critical thinking, creative problem-solving, and pattern recognition, are highly transferable to various domains, including mathematics, science, and computer programming.

By studying music theory, individuals can train their minds to approach problems with a structured and creative mindset. The problem-solving abilities fostered through music theory enhance analytical thinking, cultivate creativity, and promote a systematic approach to tackling challenges, ultimately leading to improved problem-solving skills in both musical and non-musical contexts.

Improving Spatial Reasoning Skills with Music Theory

Music theory is not only about the notes and melodies; it also involves understanding the spatial relationships between them. This emphasis on spatial reasoning makes studying music theory an effective way to enhance spatial reasoning skills.

Spatial reasoning is the ability to mentally manipulate and perceive objects in space. It is an essential skill in various domains, including mathematics, architecture, engineering, and visual arts. By engaging with music theory, individuals acquire and strengthen spatial reasoning skills that can be applied in these fields and beyond.

One way in which music theory improves spatial reasoning is through the study of musical notation. Musicians must read and decode written music, which involves understanding the spatial relationship between notes, rests, and other symbols on the musical staff. This ability to interpret and translate two-dimensional symbols into musical sounds requires mental manipulation and visualization of spatial relationships.

Additionally, music theory involves understanding intervals, which are the distances between two notes. Musicians must develop an accurate sense of interval size and be able to reproduce those intervals on their instrument accurately. This process requires mentally manipulating and perceiving spatial relationships between notes in a musical context.

Moreover, playing an instrument involves coordinating hand movements and finger placements. Musicians must navigate the spatial layout of their instrument, placing their fingers in the right positions to produce the desired notes. This spatial coordination and awareness develop fine motor skills and enhance spatial reasoning abilities.

Furthermore, music theory incorporates the concept of harmony, which involves understanding how different musical parts interact and relate to each other. Musicians must mentally visualize and manipulate the spatial relationships between harmonies, chord progressions, and voice leading. This spatial reasoning ability allows musicians to create intricate and harmonically pleasing compositions.

Research has shown a positive correlation between music training and spatial reasoning abilities. By engaging with music theory and actively participating in music-making activities, individuals can significantly improve their spatial reasoning skills. These enhanced spatial reasoning skills not only benefit musicians but also have implications in fields that require strong spatial abilities, such as mathematics, architecture, and visual arts.

Overall, studying music theory provides a unique opportunity to develop and improve spatial reasoning skills. The spatial awareness and mental manipulation required in music theory exercises the brain, leading to enhanced spatial reasoning abilities that have applications in various disciplines, fostering a well-rounded skill set.

Enhancing Pattern Recognition through Music Theory

Pattern recognition is a fundamental cognitive skill that plays a crucial role in various aspects of our lives. From understanding language to problem-solving, the ability to recognize and analyze patterns is essential. Music theory, with its intricate structure and repetitive nature, offers an excellent platform for enhancing pattern recognition skills.

One of the ways in which music theory improves pattern recognition is through the study of musical notation. Musicians learn to identify and understand the patterns created by musical symbols, such as the arrangement of notes, rests, and dynamics on the staff. This constant exposure to complex musical patterns helps to refine the brain’s ability to recognize and interpret patterns in a more intuitive and efficient manner.

Furthermore, music theory delves into the study of scales, chords, and harmonies, which are based on recurring patterns. Musicians learn to identify and internalize these patterns, which are essential for improvisation and composition. This deep understanding of musical patterns not only enhances musical proficiency but also develops the brain’s ability to recognize patterns in other domains, such as mathematics, language, and problem-solving.

Additionally, musicians gain proficiency in rhythm and meter, both of which rely heavily on the identification and repetition of patterns. Through rhythmic training, musicians develop a keen sense of timing and learn to recognize the recurring patterns of beats and accents. This heightened rhythmic awareness extends beyond music, enabling individuals to recognize and synchronize with patterns in their daily lives.

Moreover, music theory sharpens the brain’s ability to distinguish subtle variations within patterns. Musicians learn to identify the nuances of dynamics, articulation, and phrasing, which adds depth and expression to a musical performance. This acute sensitivity to subtle variations trains the brain to recognize and appreciate the intricate details within patterns, improving overall pattern recognition skills.

Research has shown a strong link between music education and enhanced pattern recognition abilities. Studies have demonstrated that musicians exhibit higher performance in tests that measure pattern recognition skills compared to non-musicians. This correlation suggests that the study of music theory has a positive impact on the brain’s ability to perceive and analyze patterns.

By engaging with music theory and actively participating in music-making activities, individuals can develop a heightened awareness and appreciation for patterns. The enhanced pattern recognition skills gained through music theory extend beyond the realm of music, enhancing cognitive abilities and enriching the overall understanding and interpretation of the world around us.

Enhancing Numerical Reasoning Skills with Music Theory

Music theory might seem like a world away from the realm of numbers and calculations, but it actually offers a unique opportunity to enhance numerical reasoning skills. The study of music theory involves understanding and manipulating numerical concepts such as intervals, rhythms, and time signatures, which can have a profound impact on developing mathematical abilities.

One way music theory enhances numerical reasoning skills is through the understanding of intervals. Musicians learn to recognize and reproduce different intervals, which are the distances between two pitches. This training fosters a strong sense of numerical relationships and spatial awareness, as musicians develop an intuitive understanding of the numerical values associated with each interval.

Additionally, music theory incorporates rhythmic notation, which represents the duration and division of time in music. Musicians must learn to interpret and perform rhythms accurately, which requires a solid grasp of fractions and subdivisions. This engagement with numerical concepts nurtures a deep understanding of mathematical relationships, as musicians develop an innate sense of timing and precision.

Moreover, music theory explores the concept of time signatures, which denote the organization of beats within a musical piece. Musicians must be able to interpret and navigate various time signatures, understanding the numerical relationships between beats and measures. This exposure to different time signatures enhances numerical reasoning skills, as musicians develop an intuitive sense of mathematical patterns and divisions.

Furthermore, music theory incorporates mathematical proportions and ratios in its study of harmony and chord progressions. Musicians learn to recognize and utilize proportional relationships between different musical elements, such as the ratios between frequencies in intervals. This exposure to mathematical principles strengthens numerical reasoning abilities and fosters an understanding of mathematical concepts beyond the realm of music theory.

Research has shown a positive correlation between music education and improved mathematical abilities. Studies have demonstrated that students who engage with music theory and actively participate in music-making activities perform better in math-related tasks compared to their non-musical peers. This suggests that the study of music theory can indeed enhance numerical reasoning skills.

Ultimately, by delving into the intricacies of music theory, individuals can enhance their numerical reasoning skills. The exposure to numerical concepts, spatial relationships, and mathematical patterns in music theory develops a strong foundation for understanding and applying mathematical principles, leading to improved mathematical abilities in various domains.

Music Theory and Mathematical Concepts

Music theory and mathematics share a deep connection, with many mathematical concepts finding expression in the realm of music. Delving into the study of music theory can provide valuable insights into mathematical principles, offering a unique perspective on the interplay between these two disciplines.

One of the key mathematical concepts embedded in music theory is the idea of patterns. Both music theory and mathematics rely on the recognition and analysis of patterns. In music theory, patterns manifest in the repetition of melodies, rhythms, and chord progressions. Similarly, in mathematics, patterns form the foundation for understanding numerical relationships and solving problems. Exploring the patterns in music theory can enhance mathematical understanding by providing real-world examples of abstract mathematical concepts.

Furthermore, music theory also aligns with mathematical concepts related to ratios and proportions. Music theory utilizes the concept of frequency ratios to define intervals and harmonies. For instance, the octave is a fundamental concept in music theory, achieved through a frequency ratio of 2:1. Similarly, in mathematics, ratios and proportions form the basis for comparison and measurement. The study of music theory offers a unique perspective on these mathematical concepts, providing a tangible and audible representation of mathematical principles.

Additionally, music theory incorporates the concept of symmetry, a fundamental element in mathematics. Symmetry plays a significant role in musical composition and is utilized to create balance and coherence. Similarly, in mathematics, symmetry is explored in geometric shapes, equations, and patterns. By studying music theory, individuals can develop an appreciation for symmetry and its implications in both music and mathematics.

Another mathematical concept evident in music theory is that of algorithms. In music theory, algorithms are utilized to create harmonic progressions, construct melodies, or generate rhythm patterns. This intersection between algorithmic thinking in music theory and mathematics highlights the shared computational nature of both disciplines. Exploring the algorithms in music theory can deepen understanding and reinforce the application of mathematical concepts in a creative and artistic context.

Moreover, music theory taps into mathematical concepts related to geometry and spatial reasoning. Musicians navigate the spatial layout of the musical staff, understanding the relationships between notes and intervals. This spatial awareness parallels the mathematical understanding of spatial relationships and geometric principles. By studying music theory, individuals can develop or enhance their spatial reasoning abilities, which can translate to improved mathematical skills.

Overall, the study of music theory provides a unique lens through which to view and understand mathematical concepts. It deepens appreciation for patterns, ratios, symmetry, algorithms, and spatial reasoning. By exploring the mathematical underpinnings of music theory, individuals can gain a richer understanding of mathematical principles while simultaneously appreciating the beauty and creativity of music.

Applying Music Theory Principles to Mathematical Problem Solving

Music theory and mathematics may seem like distinct disciplines, but they share fundamental principles that can be applied to problem-solving in both domains. By leveraging the principles and approaches from music theory, individuals can enhance their mathematical problem-solving skills and find creative solutions to complex mathematical challenges.

One of the key principles from music theory that can be applied to mathematical problem-solving is the concept of pattern recognition. In music theory, musicians develop a keen ability to recognize and interpret patterns, whether it’s identifying chord progressions or rhythmic motifs. Similarly, in mathematics, problem-solving often involves identifying patterns and relationships between numbers or variables. By applying the pattern recognition skills developed through music theory, individuals can identify underlying patterns and structures in mathematical problems, enabling them to break down complex problems into more manageable components.

Another principle from music theory that can be applied to mathematical problem-solving is the concept of abstraction. In music theory, musicians abstract the essence of a musical piece by focusing on the fundamental structures and relationships, such as intervals and chord progressions. This abstraction allows musicians to understand and perform pieces more effectively. Similarly, in mathematics, abstraction involves distilling complex problems into simpler, more abstract forms, allowing for clearer understanding and more efficient problem-solving. By leveraging the abstraction skills honed in music theory, individuals can approach mathematical problems with a more conceptual and intuitive perspective.

Additionally, music theory emphasizes creative thinking and innovation. Musicians are encouraged to experiment with melodies, harmonies, and rhythms to create unique and expressive compositions. This creative mindset can be transferred to mathematical problem-solving. Approaching mathematical problems with a creative mindset allows for the exploration of alternative approaches, unconventional perspectives, and innovative solutions. By integrating the creative problem-solving skills from music theory, individuals can approach mathematical challenges with a fresh perspective, leading to more inventive and insightful solutions.

Furthermore, music theory promotes systematic thinking and organization. Musicians learn to analyze and understand the structure and form of musical compositions. This analytical thinking can be applied to mathematical problem-solving by breaking down complex problems into smaller, more manageable steps and organizing solutions in a structured and coherent manner. By adopting the systematic thinking skills cultivated through music theory, individuals can tackle mathematical problems more effectively, ensuring clarity, accuracy, and efficiency in problem-solving processes.

Moreover, music theory emphasizes precision and attention to detail. Musicians strive for accuracy in pitch, rhythm, dynamics, and expression. This focus on precision can be applied to mathematical problem-solving by ensuring careful calculations, thorough analysis, and precise representations of mathematical concepts. The discipline and precision instilled through music theory can enhance mathematical problem-solving skills by minimizing errors and promoting rigorous thinking.

By applying the principles and approaches from music theory to mathematical problem-solving, individuals can unlock new avenues for understanding and solving complex mathematical challenges. The creative thinking, pattern recognition, abstraction, systematic organization, and attention to detail fostered through music theory provide valuable tools for approaching mathematical problems with a fresh perspective and finding innovative solutions.

Conclusion

Music theory and mathematics may appear to be distinct disciplines, but they are intricately connected, with each enhancing the other in profound ways. The study of music theory not only enriches our understanding and appreciation of music but also provides a gateway to developing and enhancing a range of cognitive and problem-solving skills.

Through music theory, individuals can enhance their cognitive skills, including memory, auditory processing, analytical thinking, creativity, and multitasking abilities. The engagement with music theory exercises the brain and nurtures these essential cognitive skills, which have far-reaching benefits beyond the realm of music.

Moreover, music theory offers a unique platform for the development of problem-solving abilities. By analyzing and interpreting musical compositions, musicians engage in critical thinking, spatial reasoning, and creative problem-solving. These skills cultivated through music theory can be transferred to other domains, enhancing problem-solving abilities in diverse fields.

In addition, music theory fosters the development of spatial reasoning skills, as musicians navigate the spatial layout of musical notation and understand the relationships between notes and intervals. The enhanced spatial reasoning abilities gained through music theory extend beyond music, benefiting various disciplines that rely on strong spatial skills.

The study of music theory also enhances pattern recognition skills, as musicians learn to identify and interpret recurring patterns in melodies, rhythms, and harmonies. These pattern recognition skills are highly transferable, improving mathematical understanding and problem-solving abilities in other domains.

Furthermore, the numerical concepts and relationships inherent in music theory deepen numerical reasoning skills. Musicians develop a keen sense of numerical relationships, proportions, and fractions through their study of music theory, strengthening their mathematical abilities and problem-solving skills.

Lastly, music theory provides insights into the connections between mathematical concepts and principles, such as patterns, ratios, symmetry, algorithms, and spatial reasoning. By exploring these connections, individuals gain a richer understanding of both music theory and mathematics, broadening their perspectives and deepening their appreciation for the beauty and interconnectedness of these disciplines.

In conclusion, the study of music theory offers far more than just knowledge of music. It provides a valuable opportunity to enhance cognitive skills, develop problem-solving abilities, improve spatial reasoning and pattern recognition, and strengthen numerical reasoning skills. The application of music theory principles to other domains, such as mathematics, opens new avenues for creative and innovative problem-solving. By embracing the overlap between music theory and mathematics, individuals can unlock their full potential, fostering a well-rounded skill set and a deeper understanding of the world around them.