What Is IC Vector In Music Theory

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for AudioLover.com, at no extra cost. Learn more)

Introduction

Music theory is a key aspect of understanding and analyzing the patterns and structures within music. It provides a framework for explaining the relationships between notes, chords, and melodies, and offers insights into the emotional and artistic impact of different musical elements. Among the many concepts in music theory, one that plays a significant role in analyzing harmonic structures is the concept of “IC vector.”

The term IC vector refers to the Interval Class Vector, which is a vital tool in understanding the distribution of intervals within a given set of pitch classes. It provides a concise representation of the intervals present in a musical composition, revealing important characteristics and aiding in the analysis of tonal relationships.

In this article, we will delve into the definition and components of IC vectors, explore how they are calculated, and discuss their practical applications in music theory. Understanding IC vectors will not only enhance your analytical skills but also offer deeper insights into the underlying harmony and structure of music.

Definition of IC Vector

An IC vector, short for Interval Class Vector, is a mathematical construct used to represent and analyze the distribution of intervals within a set of pitch classes. It serves as a concise summary that reveals the underlying harmonic relationships within a piece of music. By assigning values to specific interval classes, the IC vector provides a quantitative representation of the intervals present in a composition.

The term “interval class” refers to the grouping of intervals based on their pitch class equivalency. In other words, it disregards the specific pitch levels and focuses solely on the distance between them. For example, both a major third and a minor third are considered members of the same interval class because they share the same pitch class equivalency.

The IC vector is typically represented as an array or a sequence of numbers, where each element corresponds to the count of a particular interval class present in the musical composition. The elements of the vector are arranged in ascending order, starting from the interval class 1 (unison) and ending with the interval class 6 (tritone).

By examining the IC vector, music theorists can gain valuable insights into the harmonic content and structure of a composition. It helps identify the prevalence of specific intervals and highlights any recurring patterns or tonal relationships within the piece.

It’s important to note that the IC vector is an abstract representation of intervals and doesn’t take into account the specific pitches or their octaves. Its purpose is to provide a quantitative analysis of the intervallic relationships, allowing for a deeper understanding of the harmonic complexities present in a musical work.

Components of IC Vectors

An IC vector is composed of various elements, or components, that represent the frequencies of different interval classes within a musical composition. These components provide valuable information about the distribution of intervals and help identify the harmonic characteristics of a piece. The main components of IC vectors include:

1. Interval Class 1 (IC1) – Unison: This component represents the frequency of unisons within the composition. Unison intervals occur when two notes have the same pitch.
2. Interval Class 2 (IC2) – Semitone: The IC2 component indicates the occurrence of semitones, which are the smallest intervals in Western music. It measures the frequency of half-step intervals.
3. Interval Class 3 (IC3) – Minor Third: IC3 represents the minor third intervals, which consist of three half-steps.
4. Interval Class 4 (IC4) – Major Third: IC4 indicates the frequency of major third intervals, which comprise four half-steps.
5. Interval Class 5 (IC5) – Perfect Fourth: This component denotes the occurrence of perfect fourth intervals, which span five half-steps.
6. Interval Class 6 (IC6) – Tritone: IC6 represents the tritone intervals, which consist of six half-steps. The tritone is often referred to as the “devil’s interval” due to its dissonant and unresolved nature.

These components, ranging from IC1 to IC6, provide a comprehensive overview of the intervallic relationships within a musical composition. By analyzing the frequencies of these interval classes, music theorists can gain insights into the tension, resolution, and overall harmonic structure of a piece.

It’s important to note that IC vectors can have different lengths depending on the complexity and number of pitch classes in a musical composition. While the components mentioned above are the most commonly used, longer IC vectors may include additional interval classes to capture a wider range of harmonic information.

Interval Class (IC)

In music theory, an interval class (IC) is a concept that groups together intervals based on their pitch class equivalence. It allows us to categorize intervals that share the same melodic or harmonic function, regardless of their specific pitch or octave. By disregarding the specific pitch levels and focusing solely on the distance between them, we can identify and analyze recurring patterns and tonal relationships within a musical composition.

The concept of interval class is based on the idea that two intervals that are enharmonically equivalent, meaning they share the same pitch class, have similar melodic or harmonic qualities. For example, both a major third (C-E) and a minor tenth (C-D#) share the same pitch class equivalence of three half steps. Despite having different octaves, they are both considered members of the same interval class.

Interval classes are assigned numerical values from 0 to 6, representing the number of half steps spanned by an interval within an octave. This system simplifies the analysis and comparison of intervals, as it allows for a consistent and standardized approach. The interval class values are as follows:

1. Interval Class 0 (IC0) – Unison: This interval class represents the distance of zero half steps, meaning the interval encompasses the same pitch.
2. Interval Class 1 (IC1) – Semitone: IC1 comprises intervals that span one half step, such as a minor second or an augmented unison.
3. Interval Class 2 (IC2) – Whole Tone: IC2 consists of intervals that cover two half steps, like a major second or a whole tone.
4. Interval Class 3 (IC3) – Minor Third: IC3 includes intervals that span three half steps, such as a minor third or an augmented second.
5. Interval Class 4 (IC4) – Major Third: IC4 encompasses intervals that cover four half steps, like a major third.
6. Interval Class 5 (IC5) – Perfect Fourth: IC5 consists of intervals that span five half steps, such as a perfect fourth.
7. Interval Class 6 (IC6) – Tritone: IC6 represents intervals that cover six half steps, like a tritone.

By grouping intervals into interval classes, music theorists can better analyze and understand the harmonic structures, relationships, and tendencies within a musical piece. Interval classes provide a powerful tool for identifying recurring melodic or harmonic patterns and have practical applications in composition, analysis, and improvisation.

IC Vector Representation

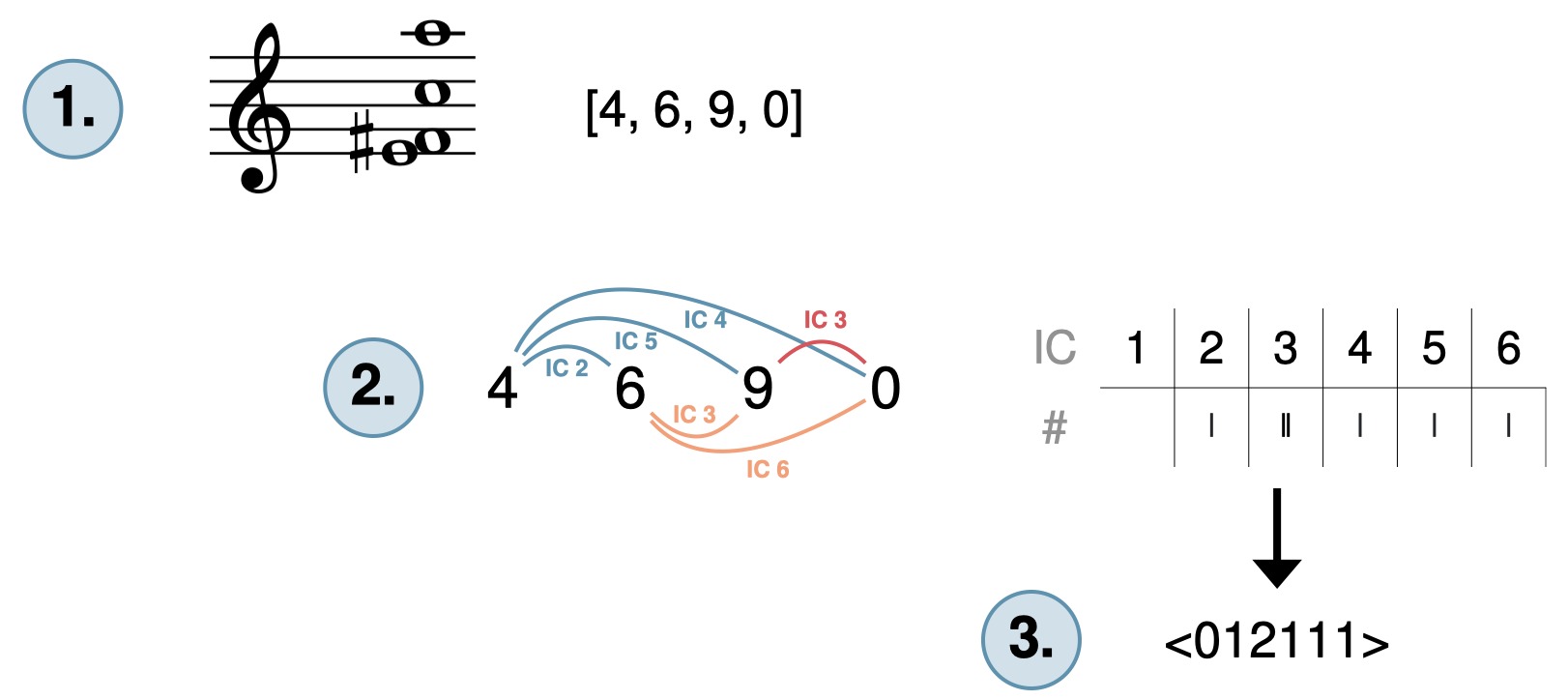
The IC vector is a concise representation of the distribution of interval classes within a musical composition. It is typically represented as an array or sequence of numbers, where each element corresponds to the count or frequency of a specific interval class. The ordering of the elements in the IC vector follows a standard convention, with the first element representing IC1, the second representing IC2, and so on, up to IC6.

For example, consider a musical composition that contains three unisons, two semitones, four minor thirds, three major thirds, one perfect fourth, and two tritones. The IC vector representation of this composition would be [3, 2, 4, 3, 1, 2].

The values in the IC vector indicate the frequency or occurrence of each interval class within the composition. They provide a quantitative measure of the relationship between different intervals, allowing for a more detailed analysis of the composition’s harmonic structure.

It’s important to note that the length of the IC vector may vary depending on the complexity and number of pitch classes present in the composition. For example, if the composition incorporates more than six different interval classes, the IC vector may expand to include additional elements to capture the additional information. However, the standard IC vector representation focuses on the most common interval classes ranging from IC1 to IC6.

By examining the IC vector representation of a musical composition, music theorists can gain valuable insights into the overall intervallic makeup of the piece. They can identify patterns, tendencies, and tonal relationships within the composition, which can then inform deeper analytical interpretations and creative decision-making processes.

Calculation of IC Vectors

To calculate an IC vector, we need to analyze the intervals within a musical composition and determine the count or frequency of each interval class. The process involves several steps:

1. Step 1: Identify the intervals: Start by identifying and labeling each interval within the composition. An interval is defined as the distance between two pitches, disregarding their specific octaves. For example, in a given musical passage, if one note is C and the other is E, the interval is a major third.
2. Step 2: Determine the interval classes: Assign each interval to its corresponding interval class based on the number of half steps it spans. Use the interval class values of IC1 to IC6, as discussed earlier, to categorize the intervals.
3. Step 3: Count the occurrences: Count the occurrences of each interval class within the composition. Keep track of how many times each interval class appears and record the counts.
4. Step 4: Create the IC vector: Arrange the interval class counts in the order of IC1 to IC6, and create an array or sequence representing the IC vector. The first element corresponds to the count of IC1, the second element represents the count of IC2, and so on.

It’s important to note that the calculation of IC vectors can be done manually or with the assistance of software programs designed for music analysis. These programs can automatically identify intervals and generate the IC vector, saving time and providing accurate results.

IC vectors serve as valuable analytical tools by summarizing the intervallic information of a musical composition. They allow for a quantitative representation of the harmonic structure, enabling music theorists and composers to gain insights into the distribution and relationships of intervals within a piece.

Application of IC Vectors in Music Theory

IC vectors play a crucial role in various aspects of music theory and analysis. They provide a quantitative representation of the intervallic relationships within a composition, allowing for deeper insights into its harmonic structure and enhancing our understanding of the piece. Here are some key applications of IC vectors in music theory:

1. Composition and Arrangement: IC vectors can be used as compositional tools to guide the creation of harmonically rich and varied musical works. By analyzing the IC vector of a composition, composers can identify patterns and tendencies, leading to more informed creative decisions in crafting engaging and well-balanced musical arrangements.
2. Harmonic Analysis: IC vectors enable music theorists and analysts to examine the distribution and prevalence of specific interval classes within a composition. This analysis sheds light on the tonal relationships, tension, and resolution within the piece. By studying the IC vector, analysts can identify tonal centers, recurring harmonic motifs, and even potential areas of dissonance or instability.
3. Comparative Analysis: IC vectors facilitate the comparison of different musical compositions or sections within a larger work. By comparing the IC vectors of two pieces, analysts can uncover similarities or differences in their harmonic structures. This comparative analysis can provide insights into the stylistic characteristics of composers or periods, as well as the influence of musical traditions or genres.
4. Modulation and Key Changes: IC vectors can aid in the analysis of modulation and key changes within a composition. By examining the changes in the IC vector between sections or movements, analysts can detect shifts in tonal centers and identify the specific interval classes that contribute to these modulations. This information can inform harmonic analysis and help explain the emotional impact of key changes.
5. Musical Education and Pedagogy: IC vectors are valuable tools in teaching music theory and analysis. They provide a visual representation of the harmonic structure and facilitate the understanding of complex musical concepts. By introducing IC vectors in music education, students can develop critical listening skills and enhance their ability to analyze and appreciate a wide range of musical genres and styles.

Overall, IC vectors have broad applications in music theory and analysis. They serve as a quantitative tool for understanding the harmonic content and structure of compositions, aiding composers, analysts, and educators in exploring and interpreting music in a more informed and nuanced manner.

Conclusion

IC vectors are a powerful tool in the realm of music theory, providing a quantitative representation of the intervallic relationships within a composition. By analyzing the distribution and frequencies of interval classes, music theorists can gain valuable insights into the harmonic content and structure of a piece of music.

The components of IC vectors, ranging from IC1 to IC6, represent different interval classes based on their pitch class equivalency. These interval classes allow for the categorization and analysis of intervals, irrespective of their specific pitches or octaves. The IC vector representation, typically in the form of an array, provides a clear and concise summary of the interval distribution within a composition.

The calculation and application of IC vectors have numerous practical benefits. Composers can use IC vectors as a compositional tool, guiding the creation of harmonically rich works. Music analysts can employ IC vectors to analyze harmonic structures, identify tonal centers, and compare compositions. Moreover, IC vectors have educational applications, helping students develop critical listening skills and enhancing their understanding of music theory.

In conclusion, understanding and utilizing IC vectors in music theory adds a new dimension to the analysis and appreciation of music. By examining the intervallic makeup of compositions through IC vectors, we can unravel the hidden harmonies, patterns, and tonal relationships that contribute to the richness and complexity of the music we encounter.