How Do Fifths Work In Music Theory

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for AudioLover.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of music theory, where the language of music comes alive and where the building blocks of musical composition are unveiled. Music theory is the study of how music works, including its structure, harmony, melody, rhythm, and notation. It provides a framework for understanding and analyzing the elements of music, allowing musicians to communicate and create music fluently.

One fundamental concept in music theory is the idea of intervals, which refers to the distance between two musical pitches. Intervals play a significant role in creating melodies, harmonies, and chords, and they form the basis for understanding the mechanics of music. In this article, we will explore one specific interval, known as the fifth, and how it functions within the context of music theory.

The fifth is a fundamental and powerful interval in music theory. It is formed by two pitches that are seven letter names apart in the musical alphabet. For instance, if we start on the note C and count up seven letters, we arrive at the note G, making the interval between C and G a perfect fifth.

Understanding the principles of fifths in music theory is essential for musicians of all levels. Whether you’re a beginner learning your first instrument or an experienced composer looking to expand your musical vocabulary, delving into the intricacies of fifths will enhance your understanding of music and open up new possibilities for creative expression.

In the following sections, we will dive deeper into the world of fifths, exploring their significance, practical applications, and how they can be utilized in chord progressions and key changes. So, let’s embark on this exciting journey through music theory to unlock the secrets of the fifth!

Basic Concepts of Music Theory

Before we delve into the world of fifths, let’s establish a foundation by exploring some basic concepts of music theory. Understanding these concepts will provide a solid framework for comprehending the role of fifths and how they interact with other musical elements.

Pitch: Pitch refers to the perceived highness or lowness of a sound. It is usually described using musical notation, which assigns letters (A-G) to different pitches. The distance between two pitches is measured in intervals.

Rhythm: Rhythm is the organization of musical sounds in time. It determines the duration and timing of notes, rests, and other rhythmic values. Rhythm gives music its groove and helps establish a sense of pulse and synchronization.

Melody: Melody is a sequence of musical notes played consecutively. It is the part of music that we typically sing or hum along to. Melodies have specific pitches, rhythms, and patterns that contribute to their overall structure and emotional impact.

Harmony: Harmony is the combination of different pitches played simultaneously, producing chords and chord progressions. It provides depth, richness, and tonal color to music. Understanding harmony is crucial for creating harmonically pleasing compositions.

Chords: Chords are groups of three or more notes played together. They provide the harmonic foundation of a piece of music and can convey different emotions and moods. Chords are built using intervals and are an essential component of music theory.

Key: A key is a specific set of notes and chords that form the basis of a piece of music. It establishes the tonal center and determines the overall mood and character of the composition. Understanding keys is crucial for understanding how different notes and chords relate to each other.

These are just a few of the basic concepts in music theory. By familiarizing yourself with these fundamentals, you will have a strong starting point for exploring the intricate world of fifths and their role in music theory.

Understanding Intervals

In music theory, intervals are the building blocks that form the foundation of melodies, harmonies, and chords. An interval represents the distance between two musical pitches, whether they are played sequentially or simultaneously. Understanding intervals is crucial for composers, musicians, and music enthusiasts, as they provide a systematic way to describe and analyze the relationships between different notes in music.

Intervals are measured in terms of their distance in pitch, which is determined by the number of letter names and accidentals (sharps or flats) between the two pitches. The simplest interval is the unison, which occurs when two pitches are identical. Moving up from the unison, we encounter various intervals such as the second, third, fourth, fifth, sixth, seventh, and octave.

Each interval has unique characteristics and qualities that influence its sound and function within a musical context. For example, a major third interval has a specific sound that creates a sense of brightness and openness, while a minor third interval has a darker, more melancholic quality.

When studying intervals, it is important to understand their size and quality. The size of an interval refers to the number of letter names or pitches it encompasses, while the quality indicates whether the interval is major, minor, perfect, augmented, or diminished. For example, a perfect fifth is a specific interval size (seven letter names), and it is considered “perfect” due to its characteristic and harmonically stable sound.

Intervals can be further categorized into consonant and dissonant intervals. Consonant intervals are considered stable and harmonious, while dissonant intervals are characterized by tension and require resolution. The perfect fifth is classified as a consonant interval and is widely regarded as one of the most stable and harmonically pleasing intervals.

Understanding intervals is crucial for various aspects of music theory, including melody writing, chord construction, and harmonic analysis. By grasping the concept of intervals, you will be equipped with the tools to create compelling melodies, harmonize effectively, and explore the rich possibilities of music theory.

Exploring Fifths in Music Theory

Now that we have a solid understanding of intervals, let’s dive into the world of fifths and their significance in music theory. The fifth is a powerful interval that plays a crucial role in harmony, chord progressions, and key relationships.

A fifth occurs when two pitches are seven letter names apart. For example, the notes C and G are a perfect fifth apart. This interval has a distinctive sound that is both stable and consonant. The perfect fifth has been used throughout centuries of music to create harmonic structures and establish tonal centers.

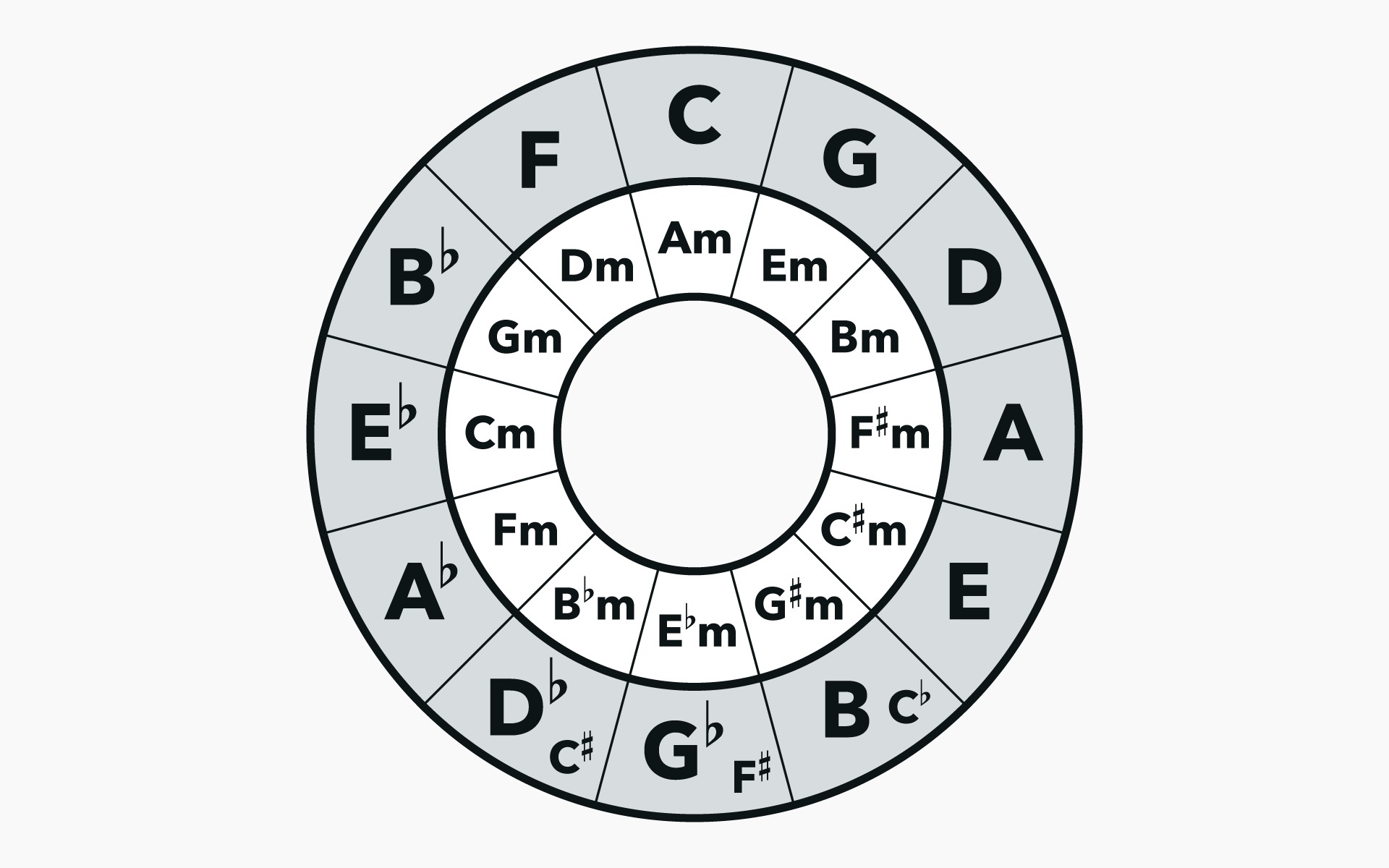
In Western music theory, the concept of the “circle of fifths” is an essential tool for understanding the relationship between different keys and chords. The circle of fifths is a diagram that arranges the twelve notes of the chromatic scale in a circular pattern, progressing through fifths clockwise.

The circle of fifths not only illustrates the relationship between keys but also reveals the common chord progressions used in music. Moving clockwise on the circle, each key adds one sharp (or subtracts one flat), resulting in a series of related keys that are a fifth apart. This progression aids in modulation, which is the act of changing keys within a piece of music.

In addition to their role in key relationships, fifths are integral to the construction of chords. The most common chord in music, the major triad, consists of a root, a major third, and a perfect fifth. The perfect fifth provides the foundation and stability in this chord, grounding the harmony and giving it a sense of completeness.

Fifths can also be used to create tension and resolution. By altering the fifth in a chord, we can introduce a sense of dissonance that requires resolution. For example, in a dominant seventh chord, the addition of a lowered fifth creates a tritone, a highly dissonant interval that yearns for resolution to a consonant chord.

Exploring the role of fifths in music theory opens up a world of possibilities for composition, improvisation, and harmonization. By understanding the harmonic relationships and structures formed by fifths, you can create rich and engaging musical experiences that evoke emotions and captivate listeners.

The Circle of Fifths

The circle of fifths is a fundamental concept in music theory, serving as a visual representation of the relationship between different keys and their corresponding chords. It is a circular diagram that illustrates the progression of keys in fifths, moving clockwise around the circle.

Starting with the key of C major (which has no sharps or flats), we move clockwise to the key of G major, which adds one sharp (F#). Continuing in this manner, we progress through the keys of D major (two sharps: F# and C#), A major (three sharps: F#, C#, and G#), and so on. Conversely, moving counterclockwise around the circle adds flats to each key.

The circle of fifths is immensely helpful for understanding the relationship between different keys. It reveals the key signatures of major and minor scales, as well as the chords commonly used in different keys. For example, in the key of C major, the circle shows that the primary chords are C, F, and G. Moving to the key of G major, the primary chords become G, C, and D.

Furthermore, the circle of fifths aids in the understanding of chord progressions. By following the circle, you can identify common progressions such as the ii-V-I progression, which is prevalent in jazz and popular music. This progression moves from the second chord in a key (ii), to the fifth chord (V), and finally resolves to the first chord (I).

The circle of fifths also helps musicians and composers determine the key relationships when modulating, or changing keys, within a piece of music. By moving along the circle, you can find closely related keys to facilitate smooth and harmonically coherent transitions. For example, if you are in the key of C major and want to modulate to the key of G major, you simply move one step clockwise around the circle.

In addition to its practical applications, the circle of fifths is a tool for analyzing and understanding harmonic relationships in music. By exploring the patterns and connections within the circle, you can gain insights into the inner workings of musical compositions and develop a deeper appreciation for the logical and mathematical aspects of music theory.

The circle of fifths is a powerful tool that connects keys, chords, and progressions in an intuitive and visually appealing way. By familiarizing yourself with this concept, you will enhance your understanding of music theory and open up new creative possibilities in your musical journey.

Using Fifths in Chord Progressions

Fifths play a crucial role in creating compelling and harmonically rich chord progressions. They provide stability and a sense of resolution, making them a powerful tool for composers and songwriters.

One common chord progression that incorporates the use of fifths is the “root-fifth” progression. In this progression, the root note of a chord is followed by its corresponding fifth. For example, in the key of C major, the root note is C, and the fifth note is G. Therefore, the progression would be C-G.

The root-fifth progression is widely used because it creates a solid and satisfying foundation for a chord progression. It is often used in combination with other chords to create more complex harmonies and arrangements.

Another way in which fifths are utilized in chord progressions is through the concept of “circle progressions.” As mentioned earlier, the circle of fifths is a diagram that represents the relationship between different keys and chords. By following the circle, you can create chord progressions that flow naturally from one key to another.

For example, starting in the key of C major, you can move to the key of G major by using the progression C – F – Bb – Eb – Ab – Db – G. Each chord in the progression is a fifth away from the previous one, creating a smooth and logical transition between keys.

Fifths also play a significant role in creating harmonic tension and resolution. By altering the fifth of a chord, you can introduce dissonance that seeks resolution to a more stable chord. This principle is commonly used in dominant seventh chords, where the lowered fifth creates a tritone interval, known for its tension and desire to resolve.

Furthermore, the use of fifths in chord progressions allows for variations and extensions to the basic triads. By adding other intervals or chords to the root-fifth progression, such as major or minor thirds, you can create more complex and intricate harmonies.

Chord progressions that incorporate fifths can be found in a variety of musical genres, ranging from classical to pop, jazz, and rock. They provide a solid foundation for melodies and allow for creative exploration and expression within the structure of a composition.

Understanding and harnessing the power of fifths in chord progressions will enhance your ability to write captivating and harmonically pleasing music. Experiment with different progressions, explore the possibilities of circle progressions, and let the stability and resolution of fifths guide your musical journey.

Modulation and Key Changes

Modulation refers to the process of changing from one key to another within a piece of music. It is a common technique used by composers to bring variety, interest, and emotional depth to their compositions. Modulating to a different key can create dramatic shifts in mood and add complexity to a musical work.

Fifths play a crucial role in facilitating smooth and coherent key changes. The circle of fifths, as mentioned earlier, provides a roadmap for modulating between closely related keys. By moving clockwise or counterclockwise on the circle, you can explore key relationships that share common tones and chords.

One common technique for modulation is the “pivot chord” or “common chord” modulation. This technique involves finding a chord that exists in both the current key and the desired key. This shared chord becomes the “pivot” and serves as a bridge between the two keys. Frequently, the pivot chord is a dominant chord, which contains the lowered fifth that creates tension and demands resolution.

For example, let’s say we are in the key of C major and want to modulate to the key of G major. We can use the dominant chord G7 (which includes the note D, the dominant seventh in the key of C) as the pivot chord. By resolving this dominant chord to the key of G major, we smoothly transition from one key to another.

Modulation through fifths can also be achieved by using a sequence of secondary dominant chords. These are dominant chords that resolve to a chord other than the tonic. By employing secondary dominants, which are typically a fifth away from the targeted chord, you can create a chain of tension and release that leads to the desired key.

The use of fifths in modulation adds a sense of musical logic and continuity to the key change. It provides a systematic and harmonic connection between keys, ensuring a smooth transition that is pleasing to the ear.

Modulation opens up a world of possibilities for composers and musicians. It allows for exploration of different moods, tonalities, and harmonic progressions, adding depth and excitement to compositions. By understanding the role of fifths in modulation, you can confidently navigate key changes and create seamless transitions that captivate listeners.

Conclusion

Understanding the role of fifths in music theory is essential for any musician or music enthusiast. The fifth is a powerful interval that provides stability, harmony, and a sense of resolution to compositions. It plays a crucial role in chord progressions, key changes, and modulation.

In this article, we explored the basic concepts of music theory, such as intervals, pitch, rhythm, melody, harmony, and chords. Building upon that foundation, we delved into the world of fifths, understanding their significance and applications within the realm of music theory.

The circle of fifths emerged as a valuable tool for visualizing key relationships, chord progressions, and modulations. By following the circle, musicians can explore related keys, create smooth transitions, and find common chord progressions that add depth and coherence to their compositions.

We also discussed the use of fifths in chord progressions, where they provide stability and a foundation for harmonies. By incorporating fifths into chord progressions, musicians can create tension and resolution, leading to captivating musical experiences.

Finally, we explored the concept of modulation and key changes. Understanding the role of fifths in modulation allows musicians to transition seamlessly between keys, adding variety, complexity, and emotional depth to their musical creations.

By embracing and utilizing the power of fifths in music theory, composers, songwriters, and musicians can unlock a world of creative possibilities. Whether it’s crafting compelling melodies, harmonizing effectively, or exploring new tonalities, fifths serve as a fundamental tool for musical expression.

So, as you embark on your musical journey, remember the significance of fifths in music theory. Harness their power, use them wisely, and let them guide you in creating harmonically rich compositions that resonate with your audience. May the power of fifths enhance your musical creations and bring joy to your musical endeavors!