How To Calculate Beat Frequency

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for AudioLover.com, at no extra cost. Learn more)

Introduction

Have you ever wondered how musicians tune their instruments to produce harmonious sounds that resonate with our emotions? Or how engineers ensure that machinery operates smoothly and efficiently? The concept of beat frequency lies at the heart of these phenomena, offering a profound understanding of the interplay between waves and oscillations.

In this comprehensive guide, we will delve into the intricacies of beat frequency, exploring its significance in various disciplines and uncovering the underlying principles that govern its calculation. Whether you are a music enthusiast, a physics aficionado, or simply curious about the fundamental forces that shape our world, this exploration of beat frequency is sure to captivate your imagination.

Through a blend of lucid explanations and real-world examples, we will unravel the essence of beat frequency, shedding light on its practical applications and theoretical underpinnings. By the end of this journey, you will have gained a deep appreciation for the role of beat frequency in shaping the symphonies of music and the symmetries of science.

Join us as we embark on an enlightening odyssey through the realm of beat frequency, where waves converge, rhythms align, and frequencies harmonize to create a tapestry of sonic and mechanical marvels. Let's unravel the mysteries and unveil the magic of beat frequency together.

Understanding Beat Frequency

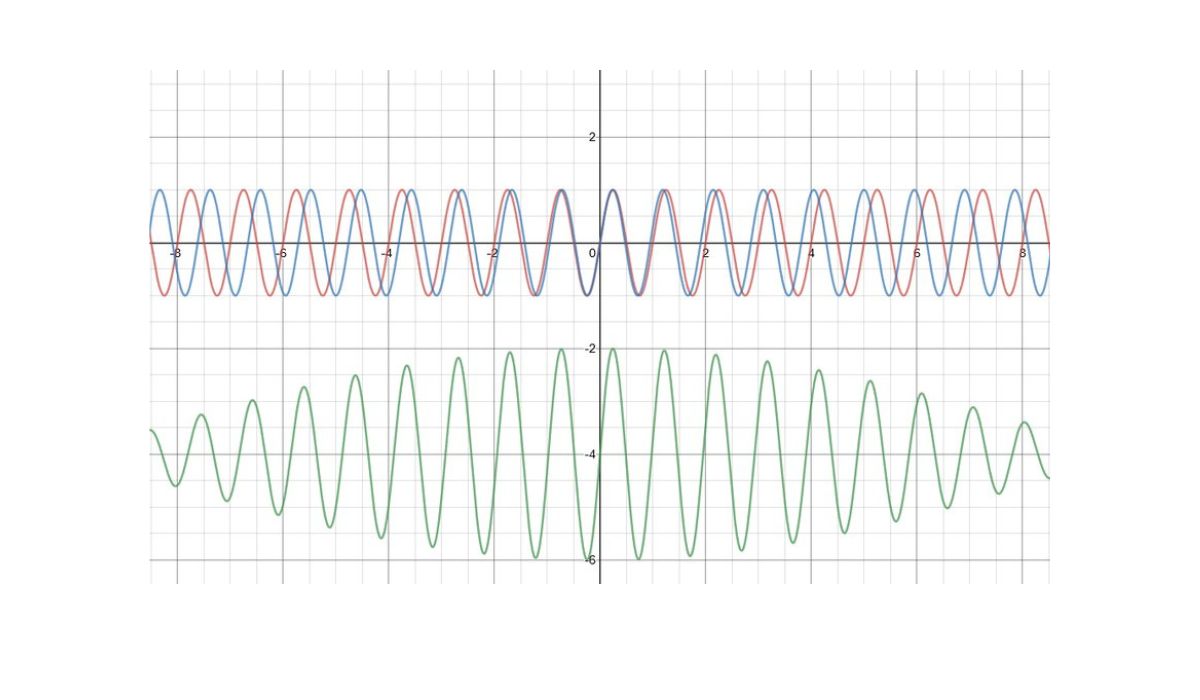
Before we delve into the intricacies of calculating beat frequency, it is essential to grasp the fundamental concept of beat frequency itself. At its core, beat frequency emerges from the interaction of two or more waves with slightly different frequencies. These waves superimpose upon each other, resulting in a phenomenon known as interference, where the peaks and troughs of the waves align or oppose each other.

When waves interfere constructively, their amplitudes combine, leading to a reinforcement of the overall signal. Conversely, when waves interfere destructively, their amplitudes cancel out, resulting in a reduction or nullification of the signal. The interplay between these constructive and destructive interferences gives rise to the perceptible phenomenon of beats, which manifests as a pulsating pattern of loudness or intensity.

From a musical standpoint, beat frequency influences the perception of consonance and dissonance in musical intervals. For instance, when two musical notes are played simultaneously, their respective frequencies create a pattern of beats that can be perceived as a pleasant or jarring sensation, depending on the alignment of the frequencies. This phenomenon forms the basis of tuning musical instruments and achieving harmonic resonance in compositions.

Furthermore, in the realm of physics and engineering, beat frequency serves as a crucial tool for analyzing and manipulating wave phenomena. Whether in the context of sound waves, electromagnetic waves, or mechanical vibrations, understanding beat frequency is indispensable for fine-tuning resonance, detecting signal interference, and optimizing the performance of various systems and devices.

By comprehending the underlying principles of beat frequency, we gain insight into the profound ways in which waves interact and influence our sensory experiences, technological innovations, and scientific explorations. This foundational understanding sets the stage for delving into the quantitative aspects of beat frequency calculation, where we will unravel the mathematical expressions that govern this captivating phenomenon.

Calculating Beat Frequency

When it comes to quantifying the pulsating rhythm of beat frequency, a straightforward mathematical approach unveils the precise relationship between the frequencies of the interacting waves. The beat frequency, denoted by f_beat, can be calculated using the simple formula:

f_beat = |f₁ – f₂|

Here, f₁ and f₂ represent the frequencies of the individual waves involved in the interference. The absolute value ensures that the beat frequency is always positive, capturing the pulsating nature of the beats regardless of the phase relationship between the waves.

It is important to note that the beat frequency is not a physical wave but rather a perceptual phenomenon arising from the interaction of waves. It signifies the rate at which the intensity or loudness of the combined wave pattern oscillates, creating the characteristic throbbing sensation perceived by our auditory faculties or instrumentation.

Furthermore, the beat frequency directly correlates with the difference in frequencies between the interacting waves. As this difference increases, the beat frequency escalates, resulting in a faster pulsation of the beats. Conversely, a smaller difference in frequencies yields a slower beat frequency, influencing the temporal pattern of the perceived beats.

By employing this straightforward formula, we can precisely quantify the beat frequency and gain a quantitative understanding of the rhythmic interplay between waves. This calculation serves as a foundational tool for musicians, physicists, engineers, and enthusiasts alike, enabling them to predict, manipulate, and harness the captivating effects of beat frequency in diverse domains.

Armed with this mathematical insight, we are poised to explore practical examples that illustrate the application of beat frequency calculation in real-world scenarios, further illuminating its significance and relevance across various disciplines.

Example Problems

Let’s delve into a few illustrative problems that showcase the application of beat frequency calculation in different contexts, ranging from music to physics and engineering. These examples will demonstrate how the concept of beat frequency manifests in diverse scenarios and how its calculation elucidates the underlying wave interactions.

• Music and Tuning: Consider two tuning forks, A and B, with frequencies of 440 Hz and 443 Hz, respectively. What is the beat frequency produced when these tuning forks are sounded together?
• Physics and Sound Waves: In a laboratory experiment, two sound waves with frequencies of 800 Hz and 805 Hz interfere with each other. What is the resulting beat frequency observed by the researchers?
• Engineering and Vibration Analysis: A mechanical system exhibits vibrations with frequencies of 1200 Hz and 1210 Hz. What is the beat frequency that engineers need to consider when optimizing the system’s performance?

By applying the formula for calculating beat frequency (f_beat = |f₁ – f₂|), we can systematically solve these problems and unveil the rhythmic patterns that emerge from the interaction of waves. These examples underscore the versatility and applicability of beat frequency across disciplines, emphasizing its role as a fundamental parameter for analyzing wave phenomena and optimizing system dynamics.

Through these practical exercises, we gain a deeper appreciation for the pervasive influence of beat frequency in shaping our acoustic experiences, scientific inquiries, and technological innovations. The ability to quantify and manipulate beat frequency empowers us to fine-tune musical compositions, unravel the properties of wave interference, and engineer efficient systems that resonate with precision and harmony.

As we navigate through these examples, we will witness the profound impact of beat frequency calculation on our understanding of wave dynamics and the orchestration of resonant frequencies in the symphony of science and engineering.

Conclusion

In conclusion, the exploration of beat frequency unveils a captivating tapestry of wave interactions, rhythmic pulsations, and perceptual phenomena that permeate diverse domains, from music and physics to engineering and beyond. By understanding the essence of beat frequency and mastering its calculation, we gain a profound insight into the subtle yet profound ways in which waves converge, interfere, and resonate to create mesmerizing patterns of intensity and harmony.

From the melodious harmonies of musical compositions to the precise orchestration of mechanical vibrations, beat frequency serves as a linchpin for understanding and manipulating wave phenomena. Its calculation, encapsulated in the simple yet powerful formula f_beat = |f₁ – f₂|, empowers us to quantify the rhythmic interplay between waves and predict the perceptible patterns of beats that captivate our senses and inform our scientific inquiries.

Furthermore, the practical examples presented in this exploration illustrate the versatility and applicability of beat frequency across disciplines, highlighting its role as a fundamental parameter for analyzing wave interactions, fine-tuning resonances, and optimizing the performance of systems and devices. Whether in the realm of musical tuning, sound wave interference, or vibration analysis, the concept of beat frequency emerges as a unifying thread that weaves through the fabric of diverse fields, enriching our understanding and enabling us to harness the rhythmic cadence of waves.

As we embrace the enchanting world of beat frequency, we embark on a journey that transcends the boundaries of disciplines and resonates with the intrinsic beauty of wave dynamics. The pulsating rhythms and harmonic resonances that emerge from the calculation of beat frequency invite us to explore, innovate, and harmonize with the symphonies of nature and technology.

With this foundational understanding, we are poised to embrace the rhythmic symmetries and resonant frequencies that shape our world, enriching our experiences, deepening our insights, and harmonizing our endeavors with the captivating cadence of beat frequency.